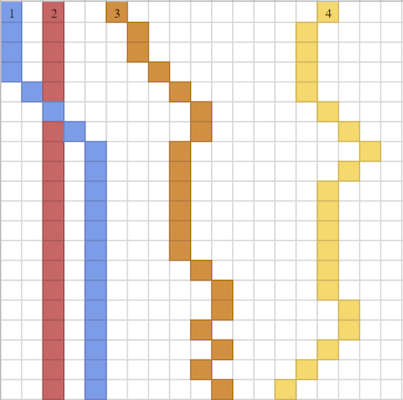Fluid Images
1 Introduction
Suppose that you are given an image and wish to shrink its width by a given number of pixels without changing its height. The simplest strategy is simply to scale the image, but this may introduce undesirable distortions. Another option is to crop the edges of the image, but this is unacceptable if the edges contain important information.
In this assignment, you will implement (in two ways) a more advanced algorithm to intelligently decide what parts of the image to remove.
2 Theme Song
Photograph by Nickelback
3 Energy
Given an image we first compute the “energy” of each pixel, which measures how much that pixel stands out from its surroundings. This gives us a rough idea of its importance. In other words, an “unimportant” pixel blends in with its surroundings, and can thus be removed with, hopefully, the least distortion to the image.
A B C |
D E F |
G H I |
use the formula
\[energy(E) = \sqrt{xenergy^2 + yenergy^2}\]
where
\[xenergy = a + 2d + g - c - 2f - i\]
\[yenergy = a + 2b + c - g - 2h - i\]
and each lowercase letter represents the brightness (sum of the red, blue, and green values) of the corresponding pixel.You are welcome to experiment with different energy functions, but the solution you hand in must use the formula above.
To compute the energy of edge pixels, you should pretend that the image is surrounded by a 1 pixel wide border of black pixels (with 0 brightness). You should use within or is-roughly to test your energy calculations since the formula includes a square root.
4 Seams
A vertical seam is a set of pixels, one from each row of the image, that are “connected” vertically. That is, any two pixels on adjacent rows are either vertically or diagonally adjacent. Note that this means seams are not always vertical lines. The energy of a seam is the sum of the energies of the pixels in the seam.
For example, in the diagram above, where each square represents one pixel, the blue (1), red (2), orange (3), and yellow (4) sets of pixels are each a seam. Note that the pixel where the blue (1) and red (2) seams overlap is in each of these seams.
We will shrink the width of the image by removing vertical seams from the picture. Our algorithm consists of repeatedly finding the lowest-energy vertical seam and removing it from the image. Sometimes multiple seams may tie for the lowest energy. If this happens, remove the leftmost of those seams. The leftmost seam refers to the seam with the leftmost pixel in the top row. For instance, in the diagram above, the blue seam (1), is the leftmost seam. If the seams overlap, the leftmost seam will be the one with the leftmost pixel in the topmost row where the seams diverge. Note that once a seam has been removed, the image has changed, so the energies of the remaining pixels must be recomputed.Think about why we remove lowest-energy seams rather than simply removing the lowest-energy pixel from each row. Better still, try it out, and you’ll see the difference for yourself! But this isn’t part of the assignment. (In principle some of these energies can just be updated, but at an introductory level, simply recomputing is sufficient.)
5 Support Code
You will be able to access the following types and functions:
Image
The image type. Has the properties width and height, which specify the dimensions of the image in pixels, and pixels, a List<List<Color>> that represents the underlying image’s data. The image object preserves only the red, green, and blue channels, ignoring the alpha channel (corresponding to transparency).
To create an image, you must first specify the dimensions of the image, and then the color of each pixel. For example:im = [image(3,2):
color(0,0,0), color(0,0,0), color(0,0,0),
color(0,0,0), color(0,0,0), color(0,0,0)]
To get the width or height of an image, you can access the following fields:im.width
im.height
To get the pixel data of an image, you can access this field:im.pixels
data Color:
| color(red :: Number, green :: Number, blue :: Number)
end
Images can be thought of as 2-dimensional lists of colors. The representation of color that you will be using for this assignment is defined above. These RGB values must be in the range between 0 and 255.
To convert a List<List<Color>> to an Image, use:
image-data-to-image(width :: Number, height :: Number, pixels :: List<List<Color>>) -> Image
Its runtime is \(O([w, h \rightarrow wh])\).The width and height must correspond to the dimensions of pixels. Here’s an example of it in use:image-data-to-image(3, 2,
[list:
[list: color(0,0,0), color(0,0,0), color(0,0,0)],
[list: color(0,0,0), color(0,0,0), color(0,0,0)]])
6 The Assignment
For this assignment, implement the following two functions:
liquify-memoization :: Image, Number -> Image
carves the number of seams given by the second parameter.
Your solution must use memoization and should be reasonably efficient: it should not take exponential time! If you cannot liquify 10 seams in a few minutes from the test images we provide, you should rethink your implementation. You do not need to be this fast to receive full credit, but it is a good benchmark.
You need to define an explicit memoize function, of the right number of parameters, and use it, to separate the core idea from the notion of memoization.
liquify-dynamic-programming :: Image, Number -> Image
This must use dynamic programming instead. Again, it must be sub-exponential.
For both of these functions, you can assume that the images will never be empty. The number of seams to carve will always be strictly less than the width of the image. This means that you never have to (and never should) deal with the “empty” image case; the image will always have pixels, since we will always leave at least 1 column of pixels remaining.
7 Test Images
All images © Shriram.
8 Built-Ins
You should be able to do this assignment with no use of mutation beyond that needed for memoization or dynamic programming. Arrays may be used only for those purposes.
In the memoization approach, this means that you should only use Arrays for the purpose of storing already-computed results that were calculated by a memoized function. In the dynamic programming approach, you should only use Arrays for the purpose of maintaining a “table” of computations.
9 Analysis
Give a big-O analysis of each solution. First find an upper bound on the total number of possible vertical seams for an image in terms of its width and height. Use this bound to find the time complexity of the naive solution, which computes the energy for every possible seam. Then determine the complexity of your two solution functions.
In your analysis, you may assume that generating the pixels from images and vice versa, for an image with width \(w\) and height \(h\), runs in \(O([w, h \rightarrow wh])\).