Updater
1 Collaboration
When working with partners, the collaboration policy applies to a pair as a whole, rather than to individuals. Indeed, you are required to collaborate.
We strongly recommend a pair-programming strategy called driver/navigator. The driver is the person with the keyboard; the navigator is the person discussing, reading each line as it’s written, and providing feedback. Every fifteen minutes, swap roles. It’s a really good habit to get used to.
Please turn in only one submission, agreeing with your partner who will do the submitting.
2 Introduction
Imagine you have a tree with arbitrary degree (that is, each node can have any number of children). You wish to modify the tree structure through a sequence of edits. For instance, the tree might represent the HTML of a Web page which you intend to change dynamically.
The simplest way to update the tree would be to copy it, incorporating the change while copying. Copying, however, takes time and space proportional to the size of the tree. If we wish to make several edits that are within close proximity of each other, perhaps we can devise a representation with lower complexity. Furthermore, we might wish to make these edits atomically, i.e., so the client sees only the result of all the edits and not the intermediate stages.
3 Theme Song
Upgrade U by Beyonce
4 Signaling Errors
In what follows, we will sometimes ask you to signal an error. You can use raise to do this [documentation]. To test for errors, uses raises [documentation].
5 The Assignment
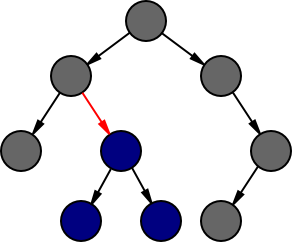
We can therefore consider representing trees in terms of a cursor, which reflects the position around which we wish to modify the tree:
A cursor represents an edge (shown in red) and has two parts: a representation of the (possibly empty) tree below that edge (shown in blue), and the (possibly empty) rest of the tree around that edge (shown in grey). The simplest representation of the part below is the subtree itself, but we have some choices in how we represent the rest of the tree, depending on which operations we wish to support. Note that a cursor can also be located above the root even though there is technically no edge above that node.
data Tree<A>:
| mt
| node(value :: A, children :: List<Tree<A>>)
end
find-cursor<A>(tree :: Tree<A>, pred :: (A -> Boolean)) -> Cursor<A>
This constructs a cursor by finding a point in a tree. The cursor represents the edge above the first node with a value for which the predicate produces true. We will assume that the search proceeds depth-first, so the cursor represents the edge above the leftmost node matching the predicate, and if there are multiple such nodes, it represents the edge above the topmost one. If find-cursor can’t find anything, signal an error with the description "Could not find node matching predicate". (Please ensure you are using this exact error message string!)
get-node-val<A>(c :: Cursor<A>) -> Option<A>
update<A>(c :: Cursor, func :: (Tree<A> -> Tree<A>)) -> Cursor<A>
Note that because we have an explicit representation for an empty node, this operation can be used to insert, change, or erase a subtree. (Erase a subtree by changing it to mt.) You would be wise to cover these operations in your test cases.
If we erase the subtree that the cursor is pointing to, the cursor
should still point to the mt subtree. It is the responsibility
of to-tree to eliminate all mt subtrees, “cleaning up”
the tree—
to-tree<A>(c :: Cursor<A>) -> Tree<A>
left<A>(c :: Cursor<A>) -> Cursor<A>
right<A>(c :: Cursor<A>) -> Cursor<A>
up<A>(c :: Cursor<A>) -> Cursor<A>
down<A>(c :: Cursor<A>, child-index :: Number) -> Cursor<A>
Note that any of these operations might fail if the cursor is at the appropriate boundary. For instance, left and right should only be able to move between edges that share a common parent. If an invalid move occurs, signal an error with the description "Invalid movement".
Critically, we want to make these four “motion” operations efficient: constant time in the number of nodes in the tree, or as close to it as possible. Can you design a data structure that achieves this? What is the complexity of the above operations that result from your representation choice? There’s an open response question about this at the end of the page; make sure you answer it by the deadline along with your program.
6 Advice
We would not be surprised if you have trouble with this assignment. Typically, students get too hung up on the efficiency part and fail to first produce a working solution. Instead, you should first consider how you would solve the problem if efficiency was not a concern, and implement that solution: you should not have too much trouble coming up with a correct solution. You can then study your solution to explore how you can improve its efficiency. You can also use the initial solution to test your later one.
The most important part of your solution is that it works correctly (even if it is inefficient) and that you analyze it correctly. If you can’t arrive at a solution that meets the efficiency requirements, you will still get partial credit for a correct analysis of an inefficient, correct solution. In contrast, you will get little to no credit for an incomplete or incorrect solution, no matter how efficient you seem to be trying to make it, or for an incomplete or incorrect analysis.
Moreover, make sure you communicate frequently with your partner when you are stuck or feel lost. It can be very helpful to bounce ideas off of each other before coming to hours or posting on the forum.
7 Testing
As always, it’s important that the tests you include in your testing file are not implementation-specific. Because you design a “custom” cursor in this assignment, any cursor one of your functions produces will be specific to your implementation and likely not meaningful to us; therefore, we can’t write tests against it. That’s why we have get-node-val and to-tree: to provide a generic way to compute values against which we can write tests.
As specified in the testing stencil, you can use get-node-val and to-tree to test all of the other functions you write. We have included some examples for you in the stencil.
Because cursor design is implementation-specific, our test suite also uses get-node-val and to-tree to test all of the required functions. Therefore, it is very important that your get-node-val and to-tree functions work correctly! We advise you to prioritize getting these functions working because, if they’re broken, every other function you write may fail tests even though it isn’t actually incorrect.
8 Analysis
Describe the run-time complexity (in big-O terms) of each of the operations in your implementation: namely left, right, up, down, update, and to-tree. Please write your analysis and upload it in the handin form. Please submit in PDF (you can use any system you want, including Word, to generate the PDF).
9 Files
Note: Implementation-dependent testing should be in the code file. The final tests file should only contain tests for the procedures we had you implement. They should run against any correct implementation, even one that adopted a different implementation strategy than your own.
10 Handing In
Please ensure only one person hands in work.